
- מְחַבֵּר Miles Stephen stephen@answers-science.com.
- Public 2023-12-15 23:36.
- שונה לאחרונה 2025-06-01 05:04.
ה משוואת קו זֶה מקבילה אוֹ בניצב לקו נתון ? תשובה אפשרית: המדרונות של קווים מקבילים שווים. החלף את השיפוע הידוע ואת הקואורדינטות של א נְקוּדָה מנגד קַו לתוך ה נְקוּדָה -צורת שיפוע ל למצוא את המשוואה של ה קו מקביל.
בהקשר זה, איך כותבים משוואה מקבילה לישר נתון?
שתיים שורות הם מַקְבִּיל אם יש להם אותו שיפוע. דוגמא 1: מצא את השיפוע של קו מקביל אל ה קַו 4x - 5y = 12. כדי למצוא את השיפוע של זה קַו אנחנו צריכים להשיג את קַו לצורת חיתוך שיפוע (y = mx + b), כלומר עלינו לפתור עבור y: השיפוע של קַו 4x - 5y = 12 הוא m = 4/5.
מהי המשוואה של קו מאונך? הנתון משוואה הוא בצורה סטנדרטית, ולכן יש להמיר אותו לצורת שיפוע-יירט: y = mx + b כדי לגלות שהשיפוע הוא -2/3. להיות אֲנָכִי השיפוע החדש חייב להיות 3/2 (היפוכו של המדרון הישן).
שנית, מהי משוואת הישר שעובר דרך המוצא ומקביל לו?
הצורה הסטנדרטית של קו היא y=mx +b. מכיוון שהקו שאנו מחפשים מקביל לאמור לעיל שאומר לנו שהשיפועים זהים. הישר שאנו רוצים את המשוואה שלו עובר דרך המקור שנותן נקודה (0, 0) ואנו יודעים את מִדרוֹן m= 2/17.
האם הקווים הללו מאונכים?
הסבר: שניים שורות הם אֲנָכִי אם ורק אם המדרונות שלהם הם הדדיים שליליים. למצוא ה מדרון, אנחנו חייבים לשים ה משוואה לצורת שיפוע-יירט,, שבו שווה ה שיפוע של השורה . לכן, כל קו מאונך חייב להיות שיפוע של.
מוּמלָץ:
איך מוצאים את משוואת הישר המאונך לנקודה אחת?

ראשית, שים את משוואת הישר הנתון לצורת שיפוע חיתוך על ידי פתרון עבור y. אתה מקבל y = 2x +5, כך שהשיפוע הוא –2. לקווים מאונכים יש שיפועים הפוכים-הדדיים, כך שהשיפוע של הקו שאנו רוצים למצוא הוא 1/2. מחברים את הנקודה שניתנה למשוואה y = 1/2x + b ופותרים עבור b, נקבל b =6
מהו השלב הראשון בבניית מאונך מנקודה לישר?
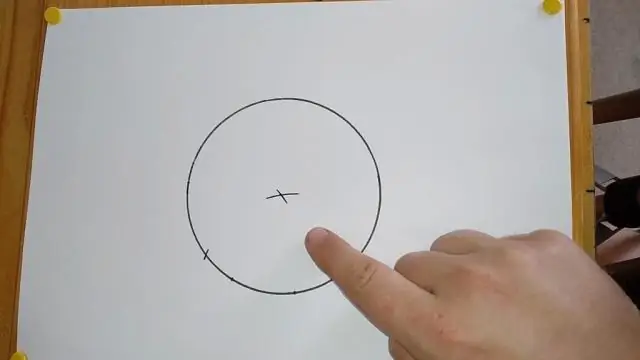
חבר את הנקודה הנתונה לנקודה שבה הקשתות מצטלבות. השתמש בקו ישר כדי לוודא שהקו ישר. הקו שאתה מצייר מאונך לישר הראשון, דרך הנקודה הנתונה על הקו
איך מוצאים את משוואת הישר בהינתן נקודה וישר מקביל?

משוואת הישר בצורת חיתוך השיפוע היא y=2x+5. השיפוע של המקבילית זהה: m=2. אז, המשוואה של הישר המקביל היא y=2x+a. כדי למצוא a, אנו משתמשים בעובדה שהקו צריך לעבור דרך הנקודה הנתונה:5=(2)⋅(−3)+a
מהי משוואת הישר המאונך לציר Y?

הסבר: ישר מאונך לציר y יהיה קו אופקי, המשוואה של כל ישר אופקי היא y=b כאשר b הוא חיתוך ה-y
האם ממוצע הוא נתון תיאורי או מסקנתי?
סטטיסטיקה תיאורית משתמשת בנתונים כדי לספק תיאורים של האוכלוסייה, בין אם באמצעות חישובים מספריים או גרפים או טבלאות. סטטיסטיקה הסקתית מביאה מסקנות ותחזיות לגבי אוכלוסייה על סמך מדגם של נתונים שנלקחו מהאוכלוסייה המדוברת
