
- מְחַבֵּר Miles Stephen stephen@answers-science.com.
- Public 2023-12-15 23:36.
- שונה לאחרונה 2025-01-22 16:59.
המחקר השיטתי הראשון של מספרים כהפשטות (כלומר, כישויות מופשטות) זוכות בדרך כלל לזכות הפילוסופים היוונים פיתגורס וארכימדס. שימו לב שמתמטיקאים יוונים רבים לא ראו ב-1 "א מספר ", אז עבורם 2 היה הקטן ביותר מספר.
באופן דומה, מי גילה מספרים שלמים?
המצרים הקדמונים הוסיפו למערכת זו כדי לכלול כל ה כוחות של 10 עד מיליון. מספרים טבעיים נחקרו לראשונה ברצינות על ידי פילוסופים ומתמטיקאים יוונים כמו פיתגורס (582-500 לפנה"ס) וארכימדס (287-212 לפנה"ס).
באופן דומה, מי מצא את המספרים 1 עד 9? כולנו יודעים ש-0 הומצא על ידי Aryabhatt. ובאשר להמצאת הספרות 1 - 9 הוא מודאג, מאמינים כי אלה הומצאו בערבית. ספרות אלו ידועות גם בשם ערבית ספרות . המערכת המספרית המיקוםית הראשונה פותחה בבבל באלף השני לפני הספירה.
נשאל גם מי יצר את מערכת המספרים?
אריאבהטה
מהי ההיסטוריה של המספרים השלמים?
ה היסטוריה של מספרים שלמים עתיק יומין כמו מושג הספירה עצמו, אבל הראשון שנכתב מספרים שלמים הופיע בין 3100 ל-3400 לפני הספירה. לפני אותה תקופה, מספרים שלמים נכתבו כסימני סיכום, ויש תיעוד של סימני סיכום המציינים מספרים שלמים המתוארכים לשנת 30,000 לפני הספירה.
מוּמלָץ:
האם מספרים שלמים הם תמיד לפעמים או לעולם לא מספרים רציונליים?

1.5 הוא מספר רציונלי שניתן לכתוב כך: 3/2 כאשר 3 ו-2 שניהם מספרים שלמים. כאן המספר הרציונלי 8 הוא מספר שלם, אבל המספר הרציונלי 1.5 אינו מספר שלם שכן 1.5 אינו מספר שלם. אז אנחנו יכולים לומר שמספר רציונלי הוא מספר שלם לפעמים לא תמיד. לפיכך, התשובה הנכונה היא לפעמים
איך חלוקת מספרים רציונליים כמו חלוקת מספרים שלמים?

פשוט תכפיל את הערכים האבסולוטיים והפוך את התשובה לשלילה. כאשר מחלקים שני מספרים שלמים עם אותו סימן, התוצאה תמיד חיובית. פשוט חלקו את הערכים האבסולוטיים והפכו את התשובה לחיובית. כאשר מחלקים שני מספרים שלמים עם סימנים שונים, התוצאה תמיד שלילית
מהם מספרים טבעיים מספרים שלמים מספרים שלמים ומספרים רציונליים?

מספרים ממשיים מסווגים בעיקר למספרים רציונליים ואי-רציונליים. מספרים רציונליים כוללים את כל המספרים השלמים והשברים. כל המספרים השלמים והמספרים השלמים מרכיבים את קבוצת המספרים השלמים. מספרים שלמים מורכבים מכל המספרים הטבעיים ואפס
איך חיסור של מספרים שלמים קשורה לחיבור של מספרים שלמים?

תשובה והסבר: הוספת מספרים שלמים פירושה הוספת מספרים שלמים עם אותם סימנים, בעוד שהפחתת מספרים שלמים פירושה חיבור שלמים של סימנים מנוגדים
האם כמה מספרים אי-רציונליים הם מספרים שלמים?
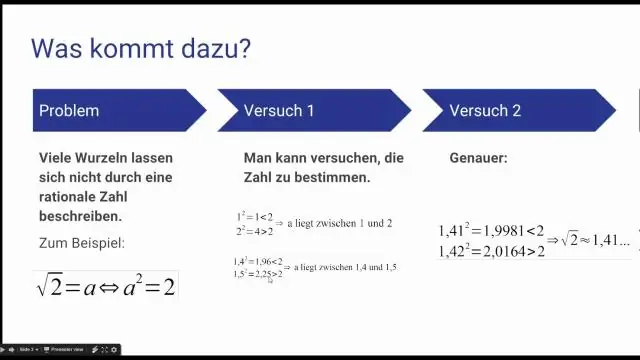
תשובה והסבר: מספרים אי-רציונליים אינם מספרים שלמים. מספר אי רציונלי הוא מספר שאינו רציונלי. במילים אחרות, לא ניתן לכתוב מספר אי-רציונלי
