
- מְחַבֵּר Miles Stephen [email protected].
- Public 2023-11-26 05:37.
- שונה לאחרונה 2025-01-22 16:59.
ארבע
יודע גם, מהי מערכת המספרים?
מערכת מספרים מייצג קבוצה בעלת ערך של מספרים שמורכב מטבעי מספרים , מספרים שלמים, אמיתי מספרים , לא הגיוני מספרים , רציונלי מספרים וממשיך. הטבעי NUMBERS : הטבעי (או הסופר) מספרים הם מ-1, 2, 3, 4, 5, 6, 7, 8, 9 וכו'. טבעי מספרים הם אינסופיים מספרים.
מלבד למעלה, מהן 3 הדוגמאות למערכות ספרות? אלו כוללים:
- מערכת ה"בסיס עשר" או "עשרונית" הרגילה: 1, 2, 3, …, 10, 11, 12, … 99, 100, ….
- ספרות רומיות: I, II, III, IV, V, VI, VII, VIII, IX, X, …
- המערכת הבינארית: 1, 10, 11, 100, 101, … (קרא כ"אחד", "אחד, אפס", "אחד, אחד", "אחד, אפס, אפס" וכו') מערכת זו המשמשת במחשב מַדָע.
בהתאם, האם קיימות מערכות מספרים אחרות?
פשוט שים, מערכת מספרים הוא א דרך לייצג מספרים . אַחֵר מְשׁוּתָף מערכות מספרים כוללים בסיס-16 (הקסדצימלי), בסיס-8 (אוקטלי) ובסיס-2 (בינארי).
מי האבא של מערכת המספרים?
פיתגורס
מוּמלָץ:
האם מספרים שלמים הם תמיד לפעמים או לעולם לא מספרים רציונליים?

1.5 הוא מספר רציונלי שניתן לכתוב כך: 3/2 כאשר 3 ו-2 שניהם מספרים שלמים. כאן המספר הרציונלי 8 הוא מספר שלם, אבל המספר הרציונלי 1.5 אינו מספר שלם שכן 1.5 אינו מספר שלם. אז אנחנו יכולים לומר שמספר רציונלי הוא מספר שלם לפעמים לא תמיד. לפיכך, התשובה הנכונה היא לפעמים
איך חלוקת מספרים רציונליים כמו חלוקת מספרים שלמים?

פשוט תכפיל את הערכים האבסולוטיים והפוך את התשובה לשלילה. כאשר מחלקים שני מספרים שלמים עם אותו סימן, התוצאה תמיד חיובית. פשוט חלקו את הערכים האבסולוטיים והפכו את התשובה לחיובית. כאשר מחלקים שני מספרים שלמים עם סימנים שונים, התוצאה תמיד שלילית
מהם מספרים טבעיים מספרים שלמים מספרים שלמים ומספרים רציונליים?

מספרים ממשיים מסווגים בעיקר למספרים רציונליים ואי-רציונליים. מספרים רציונליים כוללים את כל המספרים השלמים והשברים. כל המספרים השלמים והמספרים השלמים מרכיבים את קבוצת המספרים השלמים. מספרים שלמים מורכבים מכל המספרים הטבעיים ואפס
איך חיסור של מספרים שלמים קשורה לחיבור של מספרים שלמים?

תשובה והסבר: הוספת מספרים שלמים פירושה הוספת מספרים שלמים עם אותם סימנים, בעוד שהפחתת מספרים שלמים פירושה חיבור שלמים של סימנים מנוגדים
האם כמה מספרים אי-רציונליים הם מספרים שלמים?
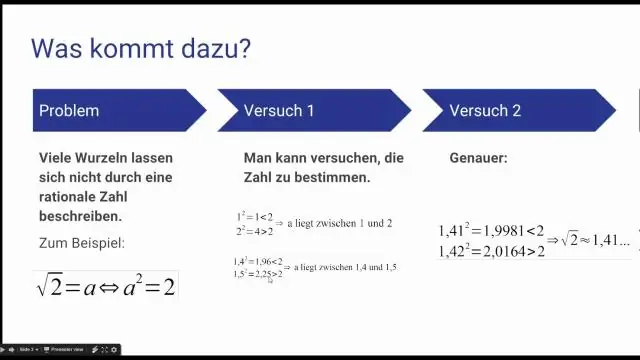
תשובה והסבר: מספרים אי-רציונליים אינם מספרים שלמים. מספר אי רציונלי הוא מספר שאינו רציונלי. במילים אחרות, לא ניתן לכתוב מספר אי-רציונלי
