איך מוצאים את הזווית המרכזית בהינתן השטח והרדיוס של גזרה?

תוכן עניינים:

קביעת הזווית המרכזית מאזור המגזר

וִידֵאוֹ: איך מוצאים את הזווית המרכזית בהינתן השטח והרדיוס של גזרה?

2024 מְחַבֵּר: Miles Stephen | [email protected]. שונה לאחרונה: 2024-01-18 08:15

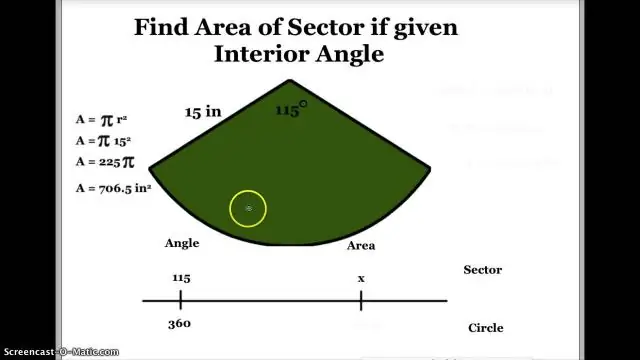
קביעת הזווית המרכזית מאזור המגזר

(πr²) × ( זווית מרכזית במעלות ÷ 360 מעלות) = אזור מגזר . אם ה זווית מרכזית נמדד ברדיאנים, במקום זאת הנוסחה הופכת:
אזור מגזר = ר² × ( זווית מרכזית ברדיאנים ÷ 2).
(θ ÷ 360 מעלות) × πr².
(52.3 ÷ 100π) × 360.
(52.3 ÷ 314) × 360.

בדרך זו, איך מוצאים את הזווית המרכזית בהינתן הרדיוס?

למצוא ה זווית מרכזית מאורך הקשת ו רַדִיוּס אתה יכול גם להשתמש ב רַדִיוּס של המעגל ואורך הקשת ל למצוא ה זווית מרכזית . קרא את המידה של ה זווית מרכזית θ. לאחר מכן: θ = s ÷ r, כאשר s הוא אורך הקשת ו-r הוא רַדִיוּס.

מלבד למעלה, איך מוצאים את הזווית המרכזית של מגזר? קביעת הזווית המרכזית מ ה מִגזָר שטח במילים אחרות: (πr²) × ( זווית מרכזית במעלות ÷ 360 מעלות) = מִגזָר אֵזוֹר. אם ה זווית מרכזית נמדד ברדיאנים, ה נוּסחָה במקום זאת הופך: מִגזָר שטח = r² × ( זווית מרכזית ברדיאנים ÷ 2).

מלבד למעלה, מהו השטח של מגזר?

ה שטח של מגזר במונחים של L ניתן לקבל על ידי הכפלת הסכום הכולל אֵזוֹר πr² לפי היחס של L להיקף הכולל 2πr.

מהי הנוסחה להיקף?

כדי לחשב את היקפו של א מעגל , השתמש בנוסחה C = πd, כאשר "C" הוא ההיקף, "d" הוא הקוטר, ו-π הוא 3.14. אם יש לך את הרדיוס במקום הקוטר, הכפל אותו ב-2 כדי לקבל את הקוטר. אתה יכול גם להשתמש בנוסחה להיקף של a מעגל באמצעות רדיוס, שהוא C = 2πr.

מוּמלָץ:

איך מוצאים את צורת הרכיב של וקטור בהינתן הגודל והזווית?

וִידֵאוֹ אם ניקח זאת בחשבון, האם 0 הוא וקטור יחידה? א וקטור יחידה הוא וֶקטוֹר שיש לו גודל של 1. הסימון מייצג את הנורמה, או הגודל, של וֶקטוֹר נגד הבסיסי וקטורים של יחידות האם אני = (1, 0 ) ו-j = ( 0 , 1) שהן באורך 1 ובעלות כיוונים לאורך ציר ה-x החיובי וציר ה-y בהתאמה.