מהי משוואת הפונקציה הריבועית?

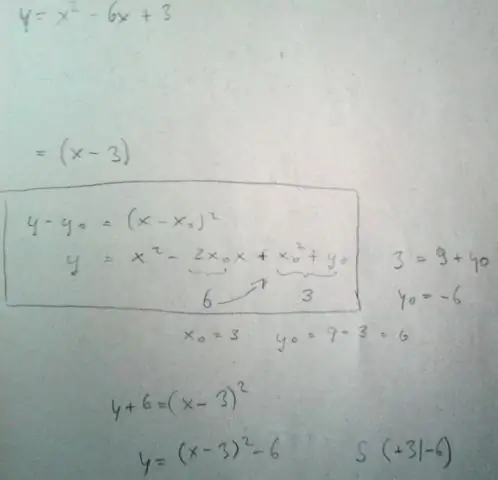
2024 מְחַבֵּר: Miles Stephen | [email protected]. שונה לאחרונה: 2023-12-15 23:36

א פונקציה ריבועית הוא אחד מהצורה f(x) = ax² + bx + c, כאשר a, b ו-c הם מספרים עם a לא שווה לאפס. הגרף של א פונקציה ריבועית היא עקומה הנקראת פרבולה. פרבולות עשויות להיפתח כלפי מעלה או למטה ולהשתנות ב"רוחב" או "התלולות", אך לכולן יש את אותה צורת "U" בסיסית.

מכאן, מהו A בצורת קודקוד?

y = a(x – h)² + k, כאשר (h, k) הוא ה קָדקוֹד . ה"א" ב- צורת קודקוד הוא אותו "א" כמו. ב-y = ax² + bx + c (כלומר, לשני ה-a יש בדיוק אותו ערך). הסימן על "a" אומר לך אם הריבוע נפתח למעלה או נפתח למטה.

איך קובעים שמשוואה היא פונקציה? זה קל יחסית לקבוע אם א משוואה היא פונקציה על ידי פתרון עבור y. כשנותנים לך א משוואה וערך ספציפי עבור x, צריך להיות רק ערך y אחד מתאים עבור אותו ערך x. לדוגמה, y = x + 1 הוא a פוּנקצִיָה כי y תמיד יהיה אחד גדול מ-x.

בדרך זו, איך כותבים משוואה לפרבולה?

ל פרבולות שנפתח לצדדים, הצורה הסטנדרטית משוואה הוא (y - k)^2 = 4p(x - h). הקודקוד או הקצה שלנו פָּרַבּוֹלָה ניתן על ידי הנקודה (ח, ק). ל פרבולות שנפתחים למעלה ולמטה, נקודת המיקוד ניתנת על ידי (h, k + p). ל פרבולות שנפתחות הצידה, נקודת המיקוד היא (h + p, k).

מהי הצורה הסטנדרטית של פונקציה ריבועית?

א פונקציה ריבועית הוא פוּנקצִיָה של תואר שני. הגרף של א פונקציה ריבועית הוא פָּרַבּוֹלָה . הכללי צורה של פונקציה ריבועית הוא f(x)=ax2+bx+c כאשר a, b ו-c הם מספרים ממשיים ו-a≠0. ה צורה סטנדרטית של פונקציה ריבועית הוא f(x)=a(x−h)2+k.