
- מְחַבֵּר Miles Stephen stephen@answers-science.com.
- Public 2023-12-15 23:36.
- שונה לאחרונה 2025-01-22 16:59.
מקרה מיוחד עבור א קופסא הוא קוּבִּיָה . זה כאשר כל הצדדים באותו אורך. אתה יכול למצוא את הנפח של a קוּבִּיָה רק על ידי ידיעת המדידה של צד אחד. כאן אנו מקבלים את המונח "קוביות".
באופן דומה, אתם עשויים לשאול, איזו צורה היא קופסה?
בעוד שספרות מתמטית מתייחסת לכל פולידרון כזה כקוביד, מקורות אחרים משתמשים ב"קוביד" כדי להתייחס ל צוּרָה מסוג זה שבו כל אחד מהפנים הוא מלבן (ולכן כל זוג פרצופים סמוכים נפגשים בזווית ישרה); הסוג המגביל יותר הזה של קוביד ידוע גם בתור מלבני, נכון
כמו כן, למה משמשת קובייה? זוהי גם צורה תלת מימדית שבה כל אחת מששת הצלעות היא ריבוע או משהו בצורת א קוּבִּיָה , כגון קרח קוּבִּיָה או בשר חתוך לתוכו קוביות ). שם העצם קוּבִּיָה חוזר למילה היוונית kybos, שהייתה למות בשש צדדים בשימוש ב משחקים. בתור פועל, קוּבִּיָה פירושו לחתוך לתוכו קוּבִּיָה צורות.
יודע גם, האם מלבן יכול להיות קובייה?
ריבוע הוא א מַלבֵּן עם כל הצדדים שווים. ריבועים סואל הם מלבנים , אבל לא כולם מלבנים הם ריבועים. באופן דומה, א קוּבִּיָה היא פריזמה מלבנית שכל הצלעות שוות, ולכן כל הפנים שווים בשטח. אז א קוּבִּיָה היא פריזמה מלבנית, אך לא כל המנסרות המלבניות קוביות.
האם קוביה היא ריבוע?
הצורה הדו-ממדית (2D) (כמו עיגול, כיכר , משולש וכו') שא קוּבִּיָה עשוי מריבועים. הצדדים (הפנים) של א קוּבִּיָה הם ריבועים. הקצוות הם קווים ישרים. הפינות (קודקודים) ישרות זוויות.
מוּמלָץ:
מה הקשר בין שטח הפנים לנפח של קובייה?

עבור קוביות קטנות מזה, שטח הפנים גדול יותר ביחס לנפח מאשר בקוביות גדולות יותר (כאשר הנפח גדול יותר ביחס לשטח הפנים). ממחיש בבירור שככל שגודלו של אובייקט גדל (מבלי לשנות צורה), היחס הזה יורד
מהו חתך רוחב של קובייה?

נקודה בודדת (קודקוד הקוביה) קטע קו (קצה הקוביה) משולש (אם שלושה פנים צמודים של הקוביה נחתכים) מקבילית (אם שני זוגות של פנים מנוגדות נחתכים - זה כולל מעוין או מלבן) טרפז (אם שני זוגות של
לכמה צדדים יש קובייה וקוביה?

גם לקוביות וגם לקוביות יש שישה פנים, 12 קצוות ושמונה קודקודים או פינות. כל קצה משותף לשני פנים. בכל קודקוד, שלושה פרצופים מתחברים זה לזה
האם אתה יכול להכפיל שורש קובייה בשורש ריבועי?

כלל המוצר שהועלה לכוח הוא חשוב מכיוון שאתה יכול להשתמש בו כדי להכפיל ביטויים רדיקליים. שימו לב שהשורשים זהים - ניתן לשלב שורשים מרובעים עם שורשים מרובעים, או שורשים קוביים עם שורשים קוביים, למשל. אבל אתה לא יכול להכפיל שורש ריבועי ושורש קובייה באמצעות הכלל הזה
איך מוצאים את הנפח של קובייה שעליה פירמידה?
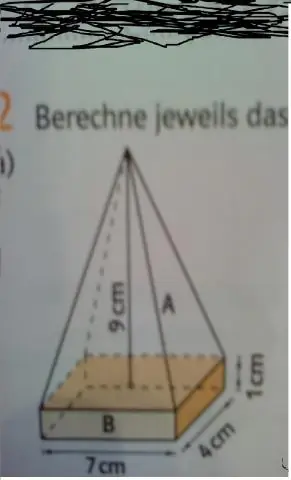
כדי למצוא את נפח הקובייה הזו, הכפל את הבסיס כפול הרוחב כפול הגובה. כדי למצוא את נפח הפירמידה, קח את שטח הבסיס, egin{align*}Bend{align*} והכפילו אותו כפול הגובה ולאחר מכן הכפל אותו ב-egin{align*}frac{1}{3}end{ יישור*}
