מהו אינסוף שורש ריבועי?

וִידֵאוֹ: מהו אינסוף שורש ריבועי?

2024 מְחַבֵּר: Miles Stephen | [email protected]. שונה לאחרונה: 2023-12-15 23:36

תשובה והסבר:

ה שורש ריבועי שֶׁל אינסוף הוא אינסוף . אם תבחר מספר ותכפיל אותו בעצמו, היה לך בריבוע המספר.

באופן דומה אפשר לשאול, מהו ריבוע האינסוף?

ה ריבוע של אינסוף ניתן לבטא כמגבלה הבאה. limx→∞√x=+∞ ומכאן כיכר שורש של אינסוף הוא אינסוף . כמו כן אנו יודעים כי ∞⋅∞=∞ מכאן שאנו מסיקים את אותה תשובה. הגבול של ה כיכר שורש אפס הוא אפס.

לאחר מכן, השאלה היא האם השורש הריבועי של 2 הוא אינסופי? כי √ 2 אינו מספר שלם ( 2 אינו מושלם כיכר ), √ 2 לכן חייב להיות לא הגיוני. ראה אי-רציונלי ריבועי או אֵינְסוֹף ירידה להוכחה שה שורש ריבועי של כל לא- כיכר מספר טבעי הוא אי רציונלי.

מכאן, מהו אינסוף חלקי אינסוף?

עם זאת, 1 מחולק לפי ∞ האם שווה גבול שמתקרב ל-0. במילים אחרות, 1 מחולק על ידי ∞ אינו שווה למספר או אינו מוגדר. כתוצאה מכך הגענו למבוי סתום. לָכֵן, אינסוף חלקי אינסוף עדיין לא מוגדר.

האם האינסוף בריבוע גדול יותר מאינסוף?

לכן אינסוף הועלה לכוחו של אינסוף יהיה גדול יותר מ "רגיל אינסוף ." אבל אינסוף בריבוע , inf * inf, מתאים למספר המספרים הרציונליים. לכן אינסוף הועלה לכוחו של אינסוף יהיה גדול יותר מ "רגיל אינסוף .”

מוּמלָץ:

מדוע y שורש ריבועי של x אינו פונקציה?

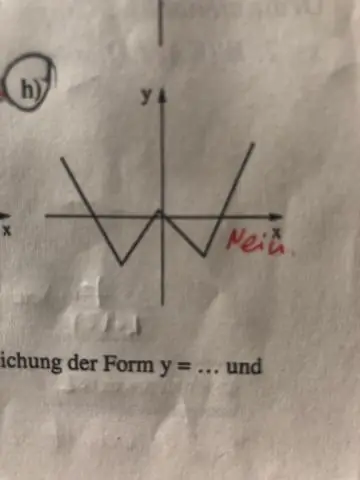
ניתן לפתור את y=x² עבור x על ידי נטילת השורש הריבועי של שני הצדדים. השורש הריבועי של מספר נותן לשניהם תשובה חיובית. x=±√y אינה פונקציה כי עבור קלט x כלשהו (או במקרה זה כמעט כל קלט x), יש שתי יציאות y שונות

האם אתה יכול להכפיל שורש קובייה בשורש ריבועי?

כלל המוצר שהועלה לכוח הוא חשוב מכיוון שאתה יכול להשתמש בו כדי להכפיל ביטויים רדיקליים. שימו לב שהשורשים זהים - ניתן לשלב שורשים מרובעים עם שורשים מרובעים, או שורשים קוביים עם שורשים קוביים, למשל. אבל אתה לא יכול להכפיל שורש ריבועי ושורש קובייה באמצעות הכלל הזה