
- מְחַבֵּר Miles Stephen stephen@answers-science.com.
- Public 2023-12-15 23:36.
- שונה לאחרונה 2025-01-22 16:59.
ב גיאומטריה היפרבולית , ישנם שני סוגים של קווים מקבילים . אם שניים קווים עושים לֹא לְהִצְטָלֵב בתוך מודל של גיאומטריה היפרבולית אבל הם מצטלבים על גבולה, אז ה שורות נקראים באופן אסימפטוטי מַקְבִּיל או היפר-מקביל.
כמו כן, אנשים שואלים, האם קווים מקבילים מצטלבים בכדור?
קווים מקבילים כן לא קיים ב כַּדוּרִי גֵאוֹמֶטרִיָה. כל ישר קַו דרך נקודה P על a כַּדוּר הוא בהגדרה מעגל גדול. שני מעגלים גדולים יהיו לְהִצְטָלֵב בשתי נקודות בקטע אוקלידי, שהוא קוטר ה- כַּדוּר . אין קווים מקבילים ב כַּדוּרִי גֵאוֹמֶטרִיָה.
כמו כן, האם קווים מקבילים יכולים להצטלב? בגיאומטריה השלכתית, כל זוג של שורות תמיד מצטלבת בשלב מסוים, אבל קווים מקבילים אל לְהִצְטָלֵב במטוס האמיתי. ה קַו באינסוף מתווסף למישור האמיתי. זה משלים את המטוס, כי עכשיו קווים מקבילים מצטלבים בנקודה השוכנת על קַו באינסוף.
יתר על כן, כמה ישרים מקבילים יש בגיאומטריה היפרבולית?
המתמטיקה שמאחורי העובדה: שניים שורות אומרים שהם מַקְבִּיל אם הם לא מצטלבים. באוקלידית גֵאוֹמֶטרִיָה , בהינתן א קַו L יש בדיוק אחד קַו דרך כל נקודה נתונה Pכלומר מַקְבִּיל ל-L (ה מַקְבִּיל הנחה). אולם ב גיאומטריה היפרבולית , יש אינסוף קווים רבים מקבילים ל-L עוברים דרך P.
מדוע אין קווים מקבילים בגיאומטריה אליפטית?
בכדורי גיאומטריה קווים מקבילים אל קיימים . באוקלידית גֵאוֹמֶטרִיָה הנחה קיים אומר את זה דרך נקודה, שם קיים רק 1 מַקְבִּיל לנתון קַו . לָכֵן, קווים מקבילים אל קיימים מאז כל מעגל גדול ( קַו ) דרך נקודה חייבים לחצות את המעגל הגדול המקורי שלנו.
מוּמלָץ:
האם אתה יכול להשתמש ב-sin ו-cos על משולשים לא ישרים?

שקול עוד משולש לא ישר, מסומן כפי שמוצג עם אורכי הצלעות x ו-y. אנו יכולים להסיק חוק שימושי המכיל רק את פונקציית הקוסינוס. ניתן להשתמש בחוק הקוסינוסים כדי למצוא את המידה של זווית או צלע של משולש לא ישר זווית אם אנחנו יודעים: שלוש צלעות וללא זוויות
כאשר חוצה חוצה שני ישרים מקבילים אילו זוגות זוויות חופפים?

אם חוצה חוצה שני ישרים מקבילים, אזי זוויות פנימיות חלופיות חופפות. אם חוצה חוצה שני קווים מקבילים, זוויות פנים של אותו צד משלימות
האם זוג קווים מצטלבים מגדיר מישור?
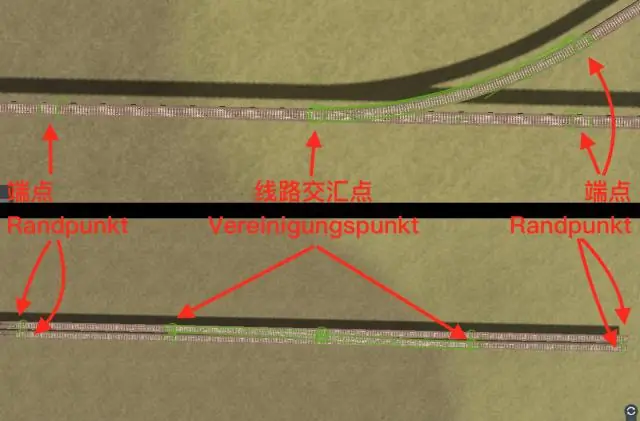
'אם שני קווים מצטלבים, אז בדיוק מישור אחד מכיל את הקווים'. 'אם שני קווים מצטלבים, אז הם מצטלבים בדיוק בנקודה אחת'. ושלוש נקודות לא קוליניאריות מגדירות מישור
מה זה קווים מצטלבים ומאונכים מקבילים?
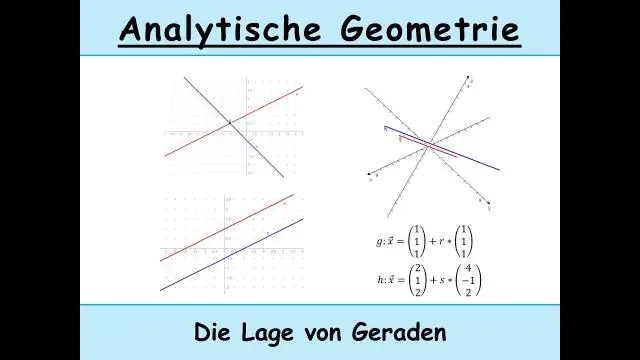
מהם קווים מצטלבים ומאונכים מקבילים? א. קווים מקבילים הם קווים במישור שנמצאים תמיד באותו מרחק זה מזה. קווים מאונכים הם קווים המצטלבים בזווית ישרה (90 מעלות)
איזה משפט מוכיח ששני ישרים מקבילים?

אם שני קווים נחתכים על ידי רוחב וזוויות מתאימות חופפות, אז הקווים מקבילים. אם שני קווים נחתכים על ידי רוחב וזוויות פנימיות חלופיות חופפות, אז הקווים מקבילים
