
- מְחַבֵּר Miles Stephen [email protected].
- Public 2023-12-15 23:36.
- שונה לאחרונה 2025-01-22 16:59.
בכללי, גבהים , חציונים , וחצוי זווית הם מקטעים שונים. עם זאת, במשולשים מסוימים, הם פחית להיות אותם קטעים. באיור, ה גוֹבַה נמשך מזווית הקודקוד של משולש שווה שוקיים פחית להוכיח שהוא א חֲצִיוֹן כמו גם חוצה זווית.
כמו כן, האם חציון יכול להיות גם גובה?
כן. א חֲצִיוֹן מחבר את נקודת האמצע של משולש עם הקודקוד הנגדי. א גוֹבַה מחבר קודקוד של משולש לצד המנוגד לקודקוד ולכן הזווית הנוצרת בין שני הקטעים היא ישרה.
שנית, האם הגובה של משולש שווה צלעות הוא גם החציון? - אם חֲצִיוֹן נמשך מקודקוד A הוא גַם חוצה הזווית, ה משולש הוא שְׁוֵה שׁוֹקַיִם כך ש-AB = AC ו-BC הוא הבסיס. מכאן זה חֲצִיוֹן הוא גַם ה גוֹבַה . ב משולש שווה צלעות , כל אחד גוֹבַה , חֲצִיוֹן וחוצה זווית נמשכת מאותו קודקוד, חופפים.
כתוצאה מכך, מה ההבדל בין גובה לחציון?
א גוֹבַה של משולש הוא האנך הנמשך מכל קודקוד לצלע הנגדית שלו ואילו a חֲצִיוֹן של משולש הוא הישר המחבר כל קודקוד ונקודת האמצע של הצלע הנגדית שלו. בתוך ה במקרה של משולש שווה צלעות חֲצִיוֹן ו גוֹבַה חופפים זה לזה.
האם החציון הוא מאונך?
1 תשובה. קטע המחבר קודקוד לנקודת האמצע של הצלע הנגדית נקרא a חֲצִיוֹן . אֲנָכִי מקודקוד לצד הנגדי נקרא גובה. קו העובר דרך נקודת האמצע של קטע והוא אֲנָכִי על הקטע נקרא ה אֲנָכִי חוצה של הקטע.
מוּמלָץ:
האם למוצקים יכול להיות pH?
בשלב המוצק, לעומת זאת, אין דבר כזה פתרון. בהגדרה, ה-pH קשור לריכוז יון המימן המומס בתמיסה. זו יכולה להיות תמיסה מימית, שבה ה-pH יכול לנוע בדרך כלל בין -2 ל-16 בערך
האם ריבוע צ'י יכול להיות שלילי?
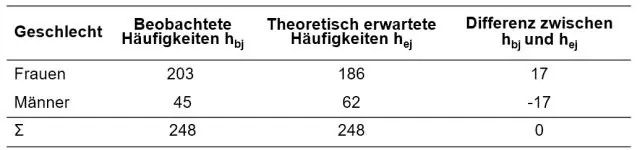
האם אתה מתכוון: האם ערכים של ריבוע צ'י יכולים להיות שליליים? התשובה היא לא. הערך של ריבוע צ'י לא יכול להיות שלילי מכיוון שהוא מבוסס על סכום של הבדלים בריבוע (בין התוצאות המתקבלות והצפויות)
האם יומן יכול להיות בעל בסיס שלילי?

לפיכך, פונקציה אקספוננציאלית עם בסיס שלילי, כמו למשל, אינה פונקציה גדולה בכלל (היא אינה רציפה), מכיוון שניתן להעריך אותה רק בערכי x מאוד ספציפיים. מסיבות כאלה אנו רואים רק לוגריתמים עם בסיסים חיוביים, מכיוון שבסיסים שליליים אינם רציפים ובדרך כלל אינם שימושיים
האם יכול להיות הר געש בלוס אנג'לס?

אין הרי געש בלוס אנג'לס. הפעילות הוולקנית הקרובה ביותר היא השדה הוולקני הלבי והשדה הוולקני קוסו
האם לגוף יכול להיות מומנטום ללא אנרגיה לתת סיבה?

תשובה והסבר: לגוף אין מומנטום ללא אנרגיה. הסיבה לכך היא שרק לאובייקטים נעים יש מומנטום, ואובייקט בתנועה תמיד הסקינטי
