וִידֵאוֹ: האם סכום סדרה אריתמטית יכול להיות שלילי?
2024 מְחַבֵּר: Miles Stephen | [email protected]. שונה לאחרונה: 2023-12-15 23:36
ההתנהגות של ה רצף אריתמטי תלוי בהבדל המשותף ד. אם ההבדל המשותף, d, הוא: חיובי, ה רצף יהיה התקדמות לקראת האינסוף (+∞) שלילי , ה רצף יהיה נסיגה לקראת שלילי אינסוף (-∞)
יתרה מכך, האם סכום סדרה יכול להיות שלילי?
אתה מדבר על סְכוּם של אינסוף סִדרָה מה שמרמז כי ה סִדרָה הוא גיאומטרי, שכן חשבון אינסופי סדרה יכולה לעולם לא מתכנסים. שימו לב, היחס המשותף חייב להיות |r| < 1 עבור א סְכוּם לצאת. כך אם היחס המשותף חיובי שם פחית להיות לא סכום שלילי.
כמו כן, מהו הסכום של סדרות אריתמטיות סופיות? ה סְכוּם של (n) מונחים של an סדרות אריתמטיות הוא (5{n}^{2}-11n) עבור כל הערכים של (n). קבע את ההבדל המשותף. ה סְכוּם של סדרות אריתמטיות הוא (ext{100}) כפול המונח הראשון שלו, בעוד שהמונח האחרון הוא (ext{9}) כפול המונח הראשון.
מזה, איך מוצאים את הסכום של סדרה אריתמטית?
ל למצוא ה סְכוּם של חֶשְׁבּוֹן רצף, התחל בזיהוי המספר הראשון והאחרון ברצף. לאחר מכן, הוסף את המספרים הללו יחד וחלק את ה סְכוּם ב-2. לבסוף, הכפל את המספר הזה במספר הכולל של האיברים ברצף ל למצוא ה סְכוּם.
מה זה N בסדרה?
המונח הראשון הוא א1, ההבדל המשותף הוא d, ומספר האיברים הוא. סכום אריתמטיקה סִדרָה נמצא על ידי הכפלת מספר האיברים כפול הממוצע של האיבר הראשון והאחרון. כדי למצוא, השתמש בנוסחה המפורשת עבור אריתמטיקה סדר פעולות . אנו פותרים 3 + (– 1)·4 = 99 כדי לקבל = 25.
מוּמלָץ:
האם למוצקים יכול להיות pH?
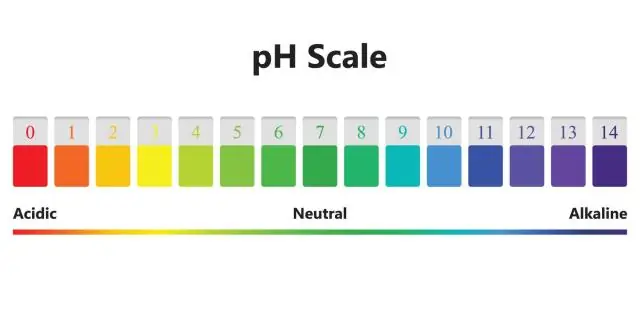
בשלב המוצק, לעומת זאת, אין דבר כזה פתרון. בהגדרה, ה-pH קשור לריכוז יון המימן המומס בתמיסה. זו יכולה להיות תמיסה מימית, שבה ה-pH יכול לנוע בדרך כלל בין -2 ל-16 בערך
האם ריבוע צ'י יכול להיות שלילי?
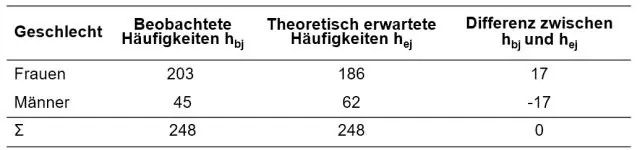
האם אתה מתכוון: האם ערכים של ריבוע צ'י יכולים להיות שליליים? התשובה היא לא. הערך של ריבוע צ'י לא יכול להיות שלילי מכיוון שהוא מבוסס על סכום של הבדלים בריבוע (בין התוצאות המתקבלות והצפויות)
האם יומן יכול להיות בעל בסיס שלילי?
לפיכך, פונקציה אקספוננציאלית עם בסיס שלילי, כמו למשל, אינה פונקציה גדולה בכלל (היא אינה רציפה), מכיוון שניתן להעריך אותה רק בערכי x מאוד ספציפיים. מסיבות כאלה אנו רואים רק לוגריתמים עם בסיסים חיוביים, מכיוון שבסיסים שליליים אינם רציפים ובדרך כלל אינם שימושיים
איך מוצאים את הסכום של סדרה אריתמטית או גיאומטרית סופית?
הנוסחה לסכום של n איברים של רצף גיאומטרי ניתנת על ידי Sn = a[(r^n - 1)/(r - 1)], כאשר a הוא האיבר הראשון, n הוא האיבר מספר ו-r הוא האיבר יחס משותף
מדוע שורש הקובייה של מספר שלילי הוא מספר שלילי?
שורש קובייה של מספר שלילי תמיד יהיה שלילי מכיוון שקוביות של מספר פירושו העלאתו לחזקה שלישית - שהיא אי זוגית - גם שורשי הקוביות של מספרים שליליים חייבים להיות שליליים. כאשר המתג כבוי (כחול), התוצאה שלילית. כאשר המתג פועל (צהוב), התוצאה חיובית