
- מְחַבֵּר Miles Stephen stephen@answers-science.com.
- Public 2023-12-15 23:36.
- שונה לאחרונה 2025-01-22 16:59.
לאחר מכן, מקדם המונח המוביל יהיה לקבוע ה התנהגות של ה פולינום . אם המשתנה (נניח X) הוא שלילי, אז ה-X במונח הדרגה הגבוה ביותר יוצר שלילי. לאחר מכן נכפיל את מקדם האיבר המוביל בשלילה ל לקבוע את התנהגות הסוף.
כמו כן, לדעת, איך אתה קובע את התנהגות הקצה השמאלי והימני?
השתמש במבחן המקדם המוביל כדי לקבוע ה סוף להתנהגות של הגרף של הפונקציה הפולינומית f(x)=−x3+5x. פתרון: מכיוון שהדרגה אי זוגית והמקדם המוביל הוא שלילי, הגרף עולה ל- שמאלה ונופל אל ה ימין כפי שמוצג באיור.
מלבד למעלה, איך מוצאים אסימפטוטים? האנכי אסימפטוטים יתרחש באותם ערכים של x שעבורם המכנה שווה לאפס: x − 1=0 x = 1 לפיכך, לגרף יהיה אנכי אסימפטוטה ב-x = 1. To למצוא האופקי אסימפטוטה , נציין שמידת המונה היא שתיים ומידת המכנה היא אחת.
בהתאם, איך אתה קובע התנהגות סופית?
ה סוף להתנהגות של פונקציה f מתארת את התנהגות של גרף הפונקציה ב"קצוות" של ציר ה-x. במילים אחרות, ה סוף להתנהגות של פונקציה מתאר את המגמה של הגרף אם נסתכל ימינה סוֹף של ציר ה-x (כאשר x מתקרב ל-+∞) ולשמאל סוֹף של ציר ה-x (כאשר x מתקרב ל-∞).
מהי התנהגות הסוף?
ה סוף להתנהגות של גרף מוגדר כמתרחש בקצה כל גרף. כשהפונקציה מתקרבת לאינסוף חיובי או שלילי, האיבר המוביל קובע איך נראה הגרף כשהוא נע לאינסוף.
מוּמלָץ:
מדוע פולינום מדרגה 2 נקרא ריבועי?
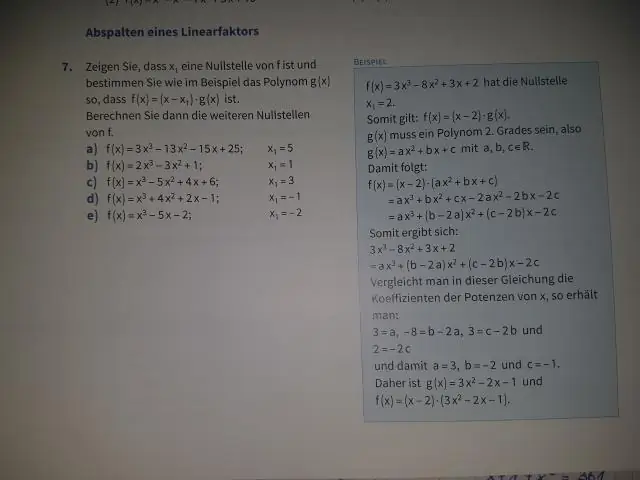
זה המקרה מכיוון שמרובע היא המילה הלטינית לריבוע, ומכיוון ששטח ריבוע באורך הצלע x ניתן ב-x2, משוואה פולינומית בעלת מעריך שני ידועה כמשוואה ריבועית ('דומה לריבוע'). בהרחבה, משטח ריבועי הוא משטח אלגברי מסדר שני
איך יודעים אם גרף פולינום חיובי או שלילי?
אם התואר אי זוגי והמקדם המוביל חיובי, הצד השמאלי של הגרף מצביע כלפי מטה והצד הימני מצביע כלפי מעלה. אם המעלה אי זוגי והמקדם המוביל שלילי, הצד השמאלי של הגרף מצביע למעלה והצד הימני מצביע למטה
מהי התנהגות הקצה של הפונקציה הפולינומית במוח?

גרף עם קצה שמאל למטה וקצה ימין למעלה. מקדם מוביל הוא שלילי ואז הקצה השמאלי למעלה והקצה הימני למטה. לכן, לפונקציה פולינומית יש דרגות אי-זוגיות והמקדם המוביל הוא שלילי
מדוע חשוב להתחשב בריבוי בעת קביעת השורשים של משוואת פולינום?

לדוגמה, מספר הפעמים שלמשוואה פולינומית נתונה יש שורש בנקודה נתונה הוא הריבוי של השורש הזה. הרעיון של ריבוי חשוב כדי להיות מסוגל לספור נכון מבלי לציין חריגים (לדוגמה, שורשים כפולים שנספרו פעמיים). מכאן הביטוי, 'נספר בריבוי'
איך מוצאים את המקדם המוביל והתנהגות הקצה?

אם המשתנה (נניח X) הוא שלילי, אז ה-X במונח הדרגה הגבוהה ביותר יוצר שלילי. לאחר מכן נכפיל את מקדם האיבר המוביל בשלילה כדי לקבוע את התנהגות הקצה
